Through discussion with fellow geometers, it seems there is a need for a simple resource showing the steps for drawing all eight semi-regular tilings of the plane using a ruler and compass, so I have compiled the methods presented here. There are, of course, many other ways to approach these tilings depending on your requirements. You can find sequential diagrams below, however if you enjoy print media or would like to support my work and help me fund further book projects, you can purchase a printed booklet version (with free UK delivery).
These tilings underpin many geometric patterns and are essential to understand if not always necessary to construct. If you need help constructing the hexagon and square you can refer to my earlier blog post about constructing regular grids with ruler and compass.

WHAT IS A SEMI-REGULAR TILING?
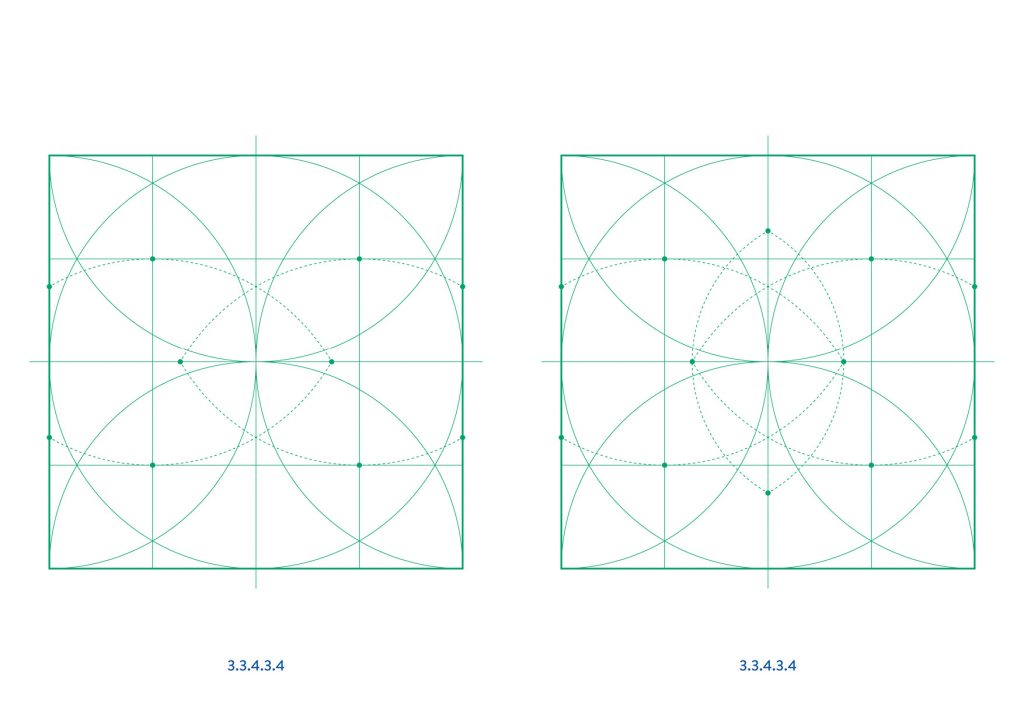
Semi-regular tilings, also known as Archimedean tilings, are infinite tilings of the two-dimensional plane comprised of more than one regular polygon, where each vertex in the tiling is surrounded by the same set of polygons, in the same order. These can all be constructed using simple ruler and compass methods as demonstrated here.
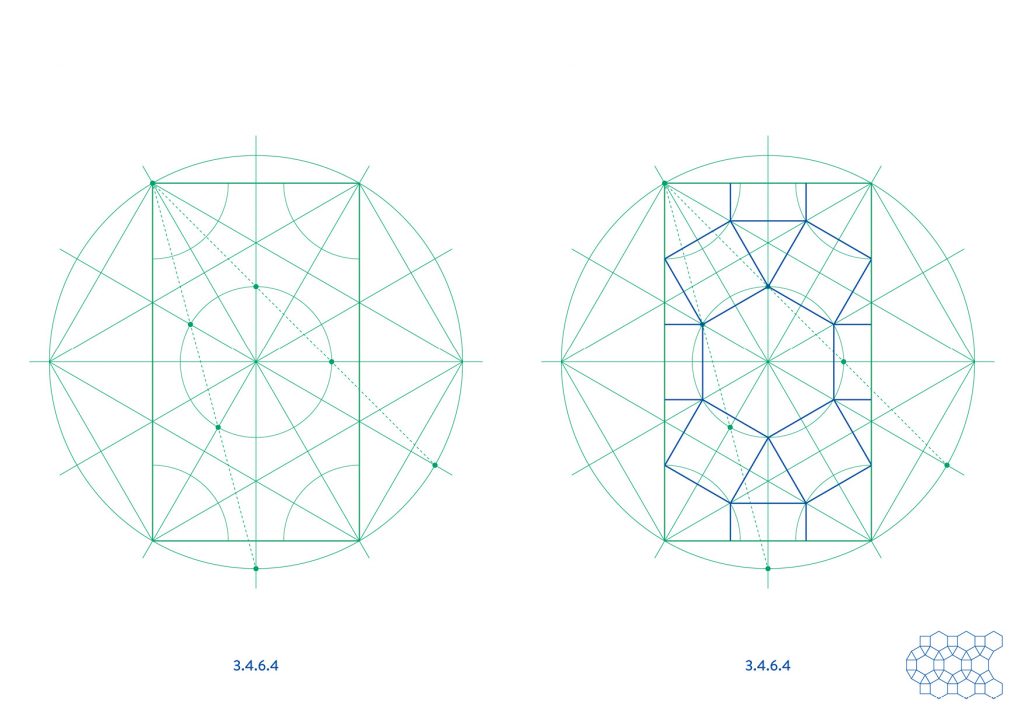
The notation used to define each tiling describes the sequence of polygons around each vertex. Hence 3.4.6.4 means that each vertex has a cluster of triangle, square, hexagon, square positioned around each vertex, in that order.
Uniform tilings are those which have a single vertex condition, meaning the same grouping of polygons are clustered around each vertex. These include the three regular tilings, 6.6.6 (hexagonal or honeycomb), 4.4.4.4 (square) and 3.3.3.3.3.3 (triangular or isometric) and eight further semi-regular tilings. These are the focus of this post.
An infinite number of tilings can be generated using regular polygons if the vertex rule is relaxed. These are called n-uniform tilings, where n denotes the number of different vertex conditions in the tiling.
TESSELLATION
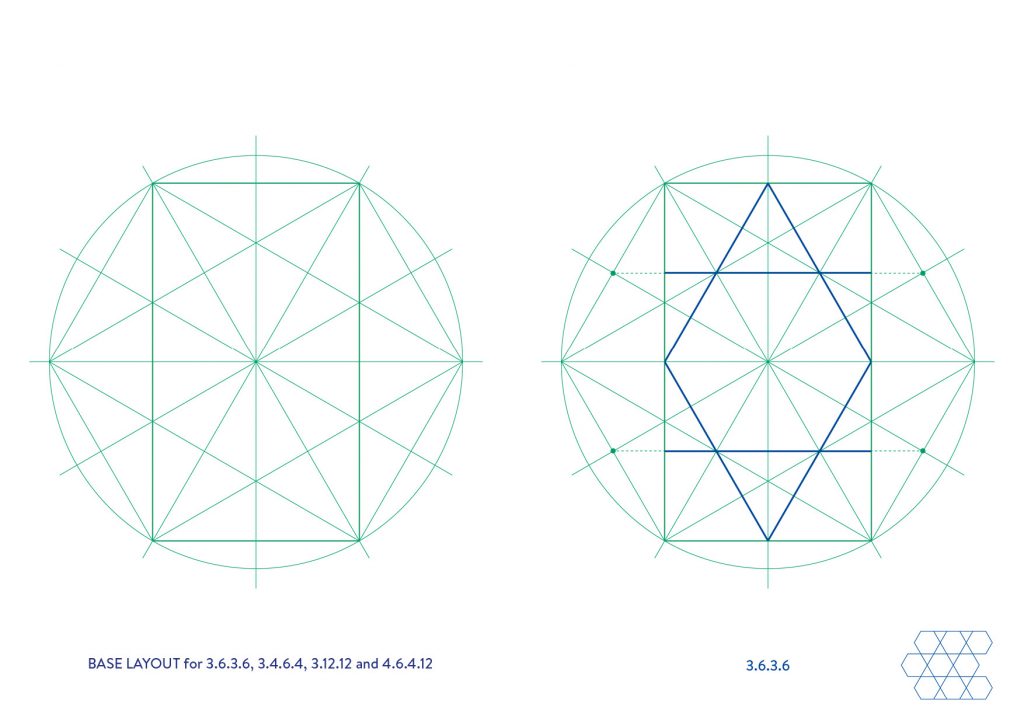
The methods presented here aim to work from the outside in with as succinct construction as possible, rather than expanding a grid out from the centre. In all but one case the result is a simple, repeatable rectangular or square unit.
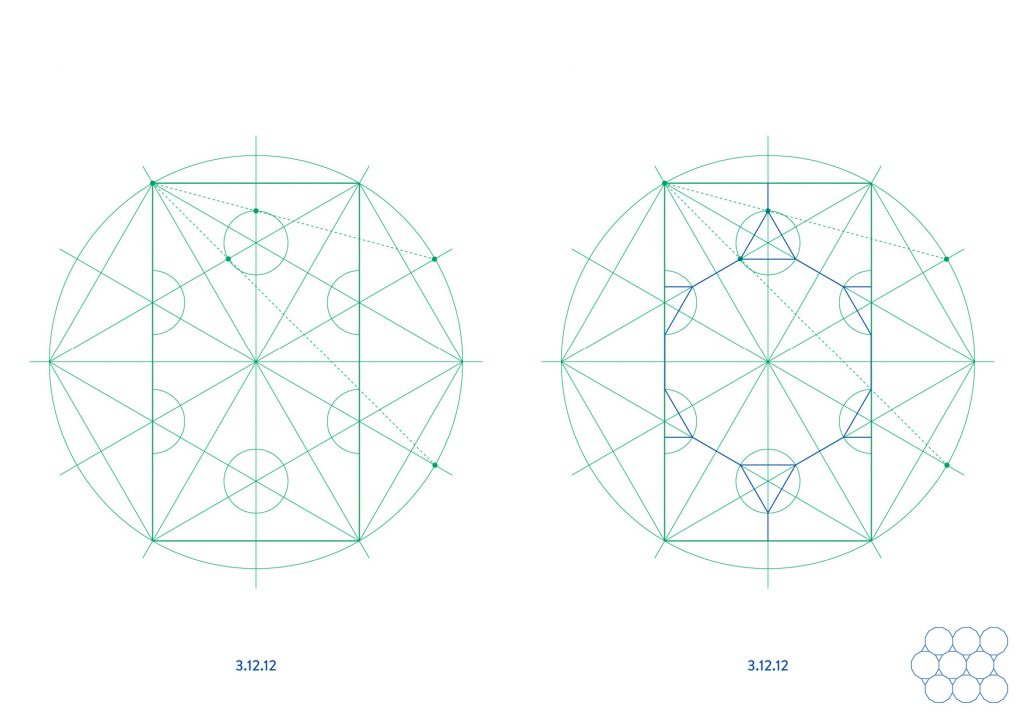
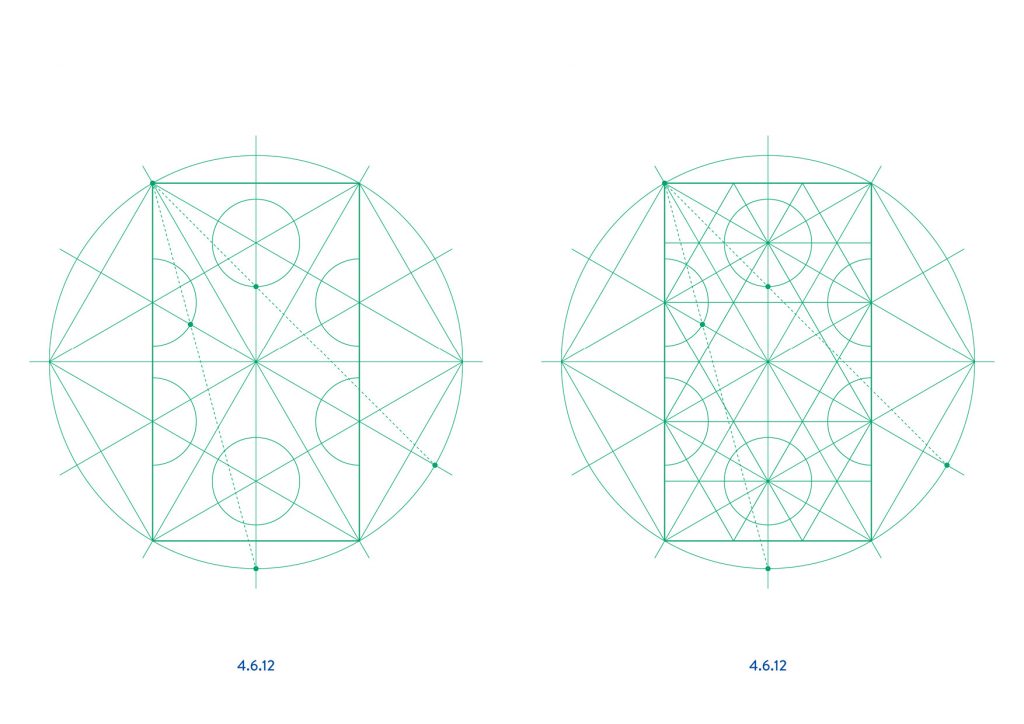
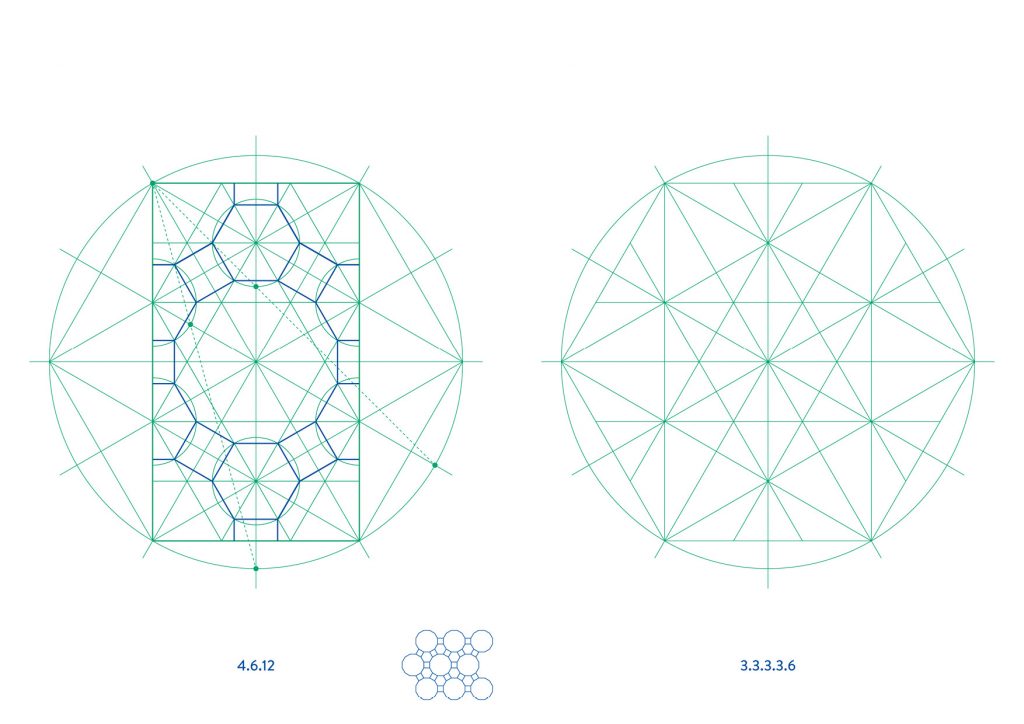
The first four tilings, 3.6.3.6, 3.4.6.4, 3.12.12 and 4.6.12, all repeat in a rectangle of 1:√3 proportions and can therefore be constructed from the base layout in the first diagram.
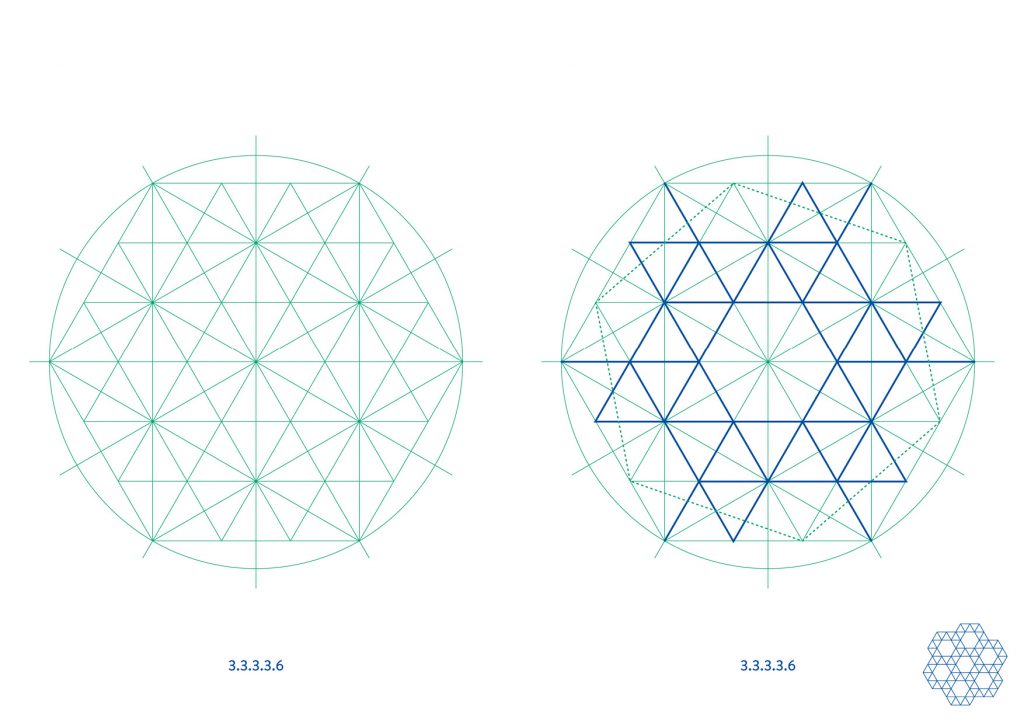
The 3.3.3.3.6 tiling repeats with an unusual offset. The dotted line shows a hexagonal unit which can be repeated by translation. An easier option is to construct this tiling on a wider isometric grid.
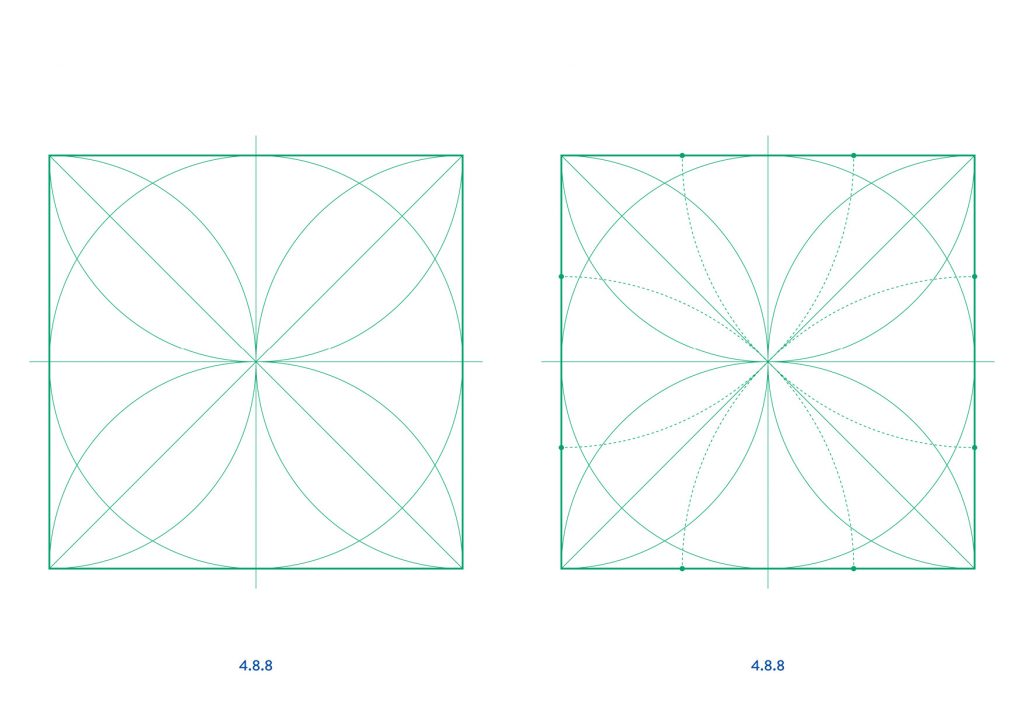
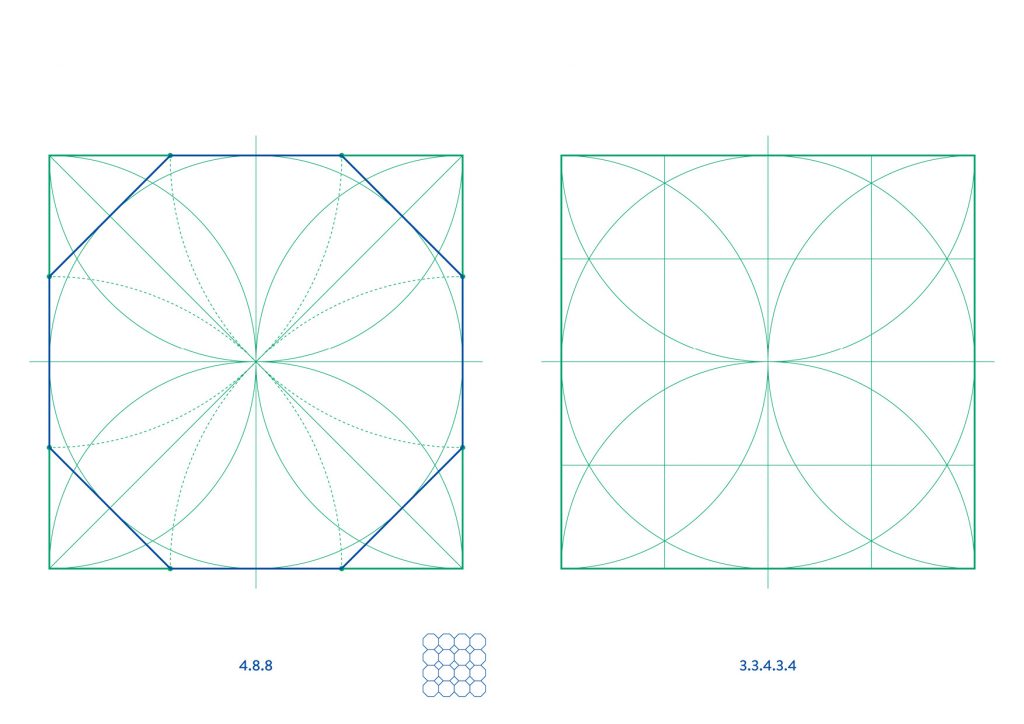
4.8.8 and 3.3.4.3.4 both repeat in a square unit.
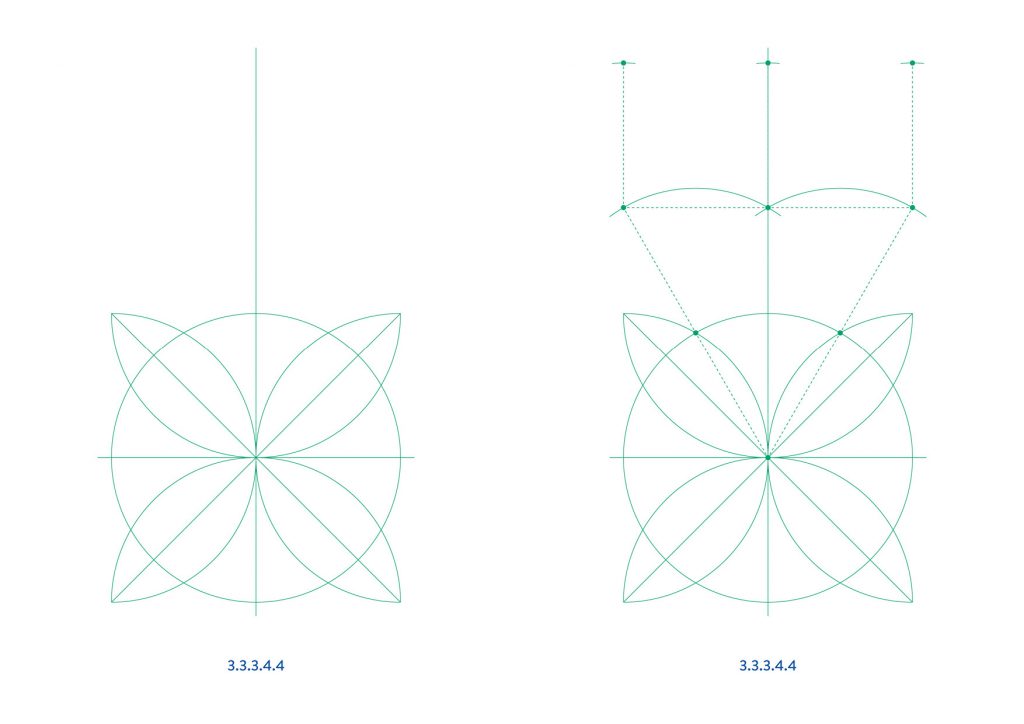
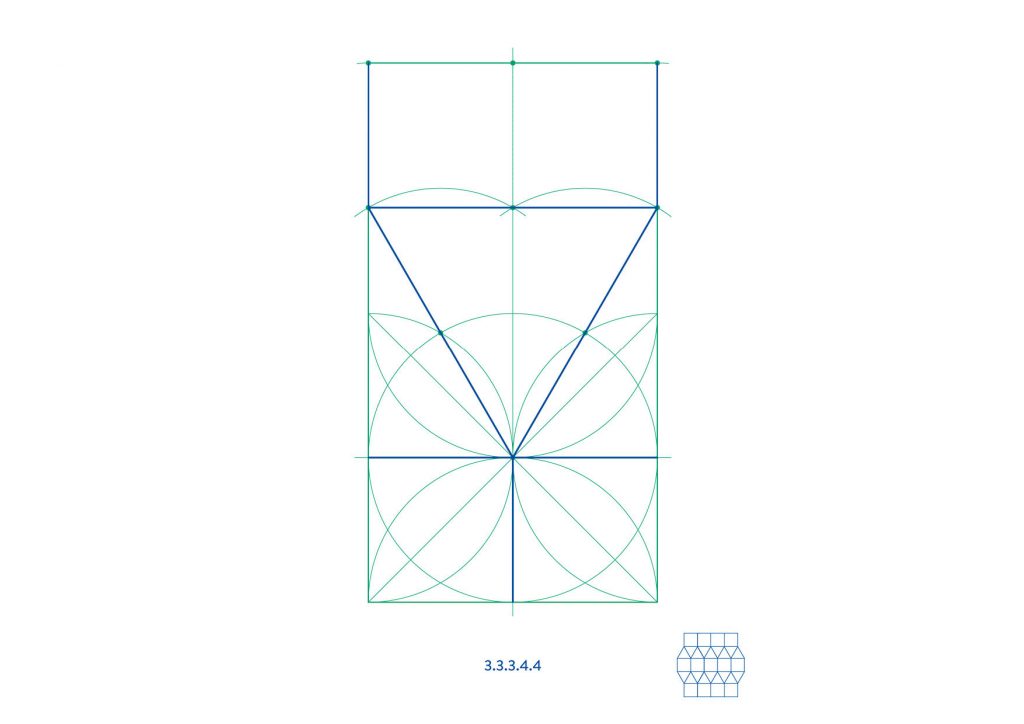
The final tiling, 3.3.3.4.4, must be reflected to repeat seamlessly. Alternatively, another vertically reflected tile can be constructed to create a tall rectangular unit which can be repeated by translation.
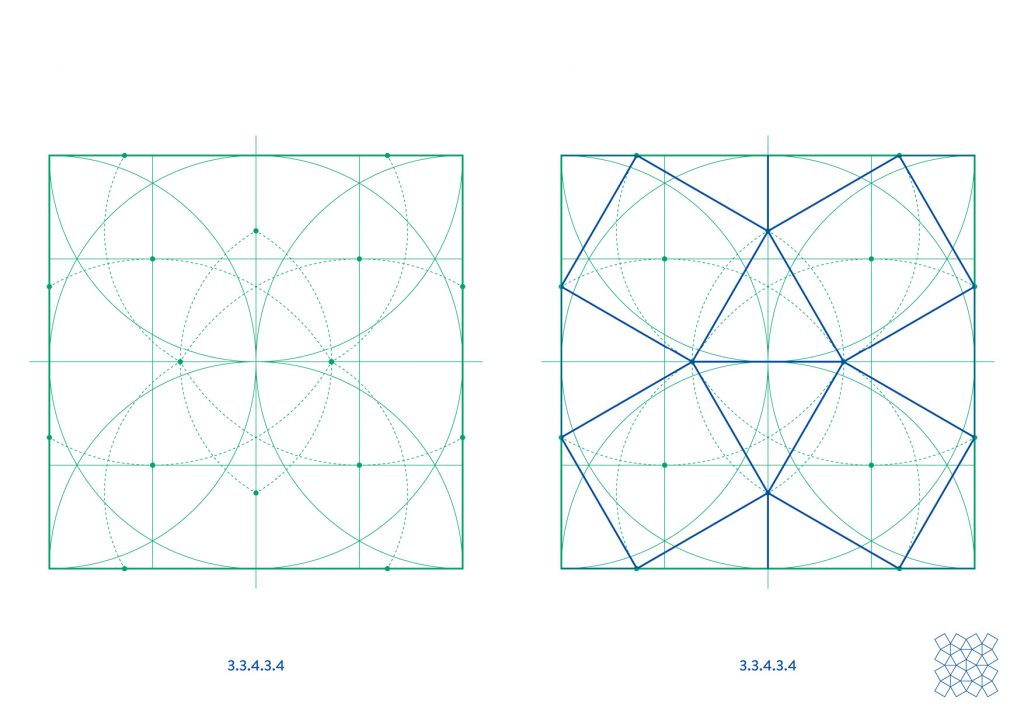
Dual Tilings
The dual tilings (also referred to as Catalan or Laves tilings) are generated by connecting the centres of each tile in the semi-regular tilings and passing through the midpoint of each edge. As there is only one vertex condition in the semi-regular tilings, the duals are each comprised of a single shape.
This content is made available under a Creative Commons Attribution-Non Commercial-ShareAlike License CC BY-NC-SA 4.0
Further Reading
Ruler & Compass – Andrew Sutton (published Wooden Books)
Tilings & Patterns – Branko Grunbaum & G.C. Shephard (published by Dover Books)


Thank you!