Abstract
This paper examines the development and use of vocabularies of shapes constructed using geometric principles as a basis for ornamental pattern design. Through a combination of digital fabrication techniques and printmaking, I have developed a process for freely exploring geometric ornamentation based on compatible vocabularies of shapes. The process highlights the correlation between the use of these vocabularies and language as a medium of expression. It can also give an insight into how the universality of the visual expression of mathematical concepts helps us perceive the nature of the world around us.
LINK TO THE ORIGINAL PAPER – the full article is also reproduced below
Introduction
‘Geometry is an inexhaustible well of formal beauty from which to fill our bucket; but before the draught is fit for use it should be examined, analysed and filtered through the consciousness of the artist.’ (Bragdon, 1915)
Geometric and mathematical principles have provided a structural foundation for ornamental art and design in cultures across the world since antiquity. Although this approach was developed in many different cultures throughout history, within the Islamic artistic tradition it has been taken to sophisticated heights of expression, mainly in the context of architecture and the book arts. In this article I will be discussing the use of geometric ornamentation as a visual language. Through practice-based research, I have discovered how a visual lexicon of shapes developed from geometric principles can be used to explore the concept of beauty expressed through harmony, symmetry and mathematical proportion in design.
Islamic geometric patterns are fundamentally based on the regular division of the circle (El-Said and Parman, 1976). The circle can be defined as a two-dimensional figure in which all points are equidistant from a single indefinably small point, the centre. A series of regularly spaced points on the circumference can be joined with straight lines to generate regular polygons (i.e. shapes with equal length sides and equal internal angles). Hence all the regular polygons arise from the regularly divided circle. Symbolically this idea represents unity in multiplicity – the whole represented in the many (Burckhardt and Michaud, 1976). The omnipresent centre is connected to the infinite and unbounded, expressed in endlessly repeating patterns based on pure mathematical truths and timeless archetypal forms.
From a regularly divided circle a network of interconnected star motifs can be constructed following a method similar to the one outlined in fig 1. This principle forms the core of an infinite range of possibilities, including the combination of stars with different numbers of points in one pattern and allowing for the construction of different geometric star motifs.

Traditionally geometric patterns were drawn with the ancient tools of compass and straightedge (an unmarked ruler). These allow for the physical construction of the Euclidean ideals of line and circle, or arc. An exploration of the interaction of line and arc leads to a form of visual mathematics from which a focussed visual language has grown. Despite the often complex appearance of the patterns, practically they are an application of the axioms and postulates defined by Euclid in a series of books, The Elements (Byrne and Oechslin, 2010). Pythagoras’ theorem and simple trigonometry also provide a useful basis for understanding the patterns.
Islamic geometric design is both a practical application of geometric principles in craft practice as well as a metaphysical form of expression. A remarkably varied but consistent visual language developed across a huge geographical spread, from Spain to Central Asia, and a timeframe of over a thousand years. This was built on the long-standing ornamental traditions and mathematical discoveries of Persia, India, China, Rome and Greece, all of which incorporated geometric principles into their art and architecture.
There is a commonly held idea that the predilection towards geometry within Islamic art is a response to the prohibition of the representation of figurative forms. That a negative influence could result in the flourishing of such a diverse and sophisticated visual language does an injustice to the cohesive development of this artform. It is perhaps more accurate to say that the visual representation of number through geometry communicates key aspects of Islamic spirituality in a way that representations of the material world never could (Burckhardt and Michaud, 1976; Wichmann and Wade, 2017). While this is an interesting aspect in the development of Islamic geometric design as a whole, this paper will focus on the development and use of vocabularies of geometric forms in ornamental pattern.
Developing a visual vocabulary
Over the past five years my visual research has focussed on Islamic geometric design and I have explored its application largely through drawing, printmaking and animation. Here I will present the development of an ongoing project which has allowed me to explore the structural possibilities of geometry within a visual and process-led framework. It has also allowed me to tap into an ancient tradition of design and explore it with the tools available today and the possibilities they offer.
The project began with research into a family of patterns which exhibit fivefold symmetry (i.e. the same elements are repeated five times when rotated around a common centre). The first issue I encountered was how to tile motifs based on this symmetry, for example, the ten-pointed star [fig 1]. The only regular polygons which can tile the two-dimensional plane by themselves are the triangle, square and hexagon. Attempting to tile pentagons or decagons (a regular ten-sided polygon) results in gaps which need other shapes to fill them [fig 2]. Johannes Kepler (Kepler et al., 1997) and Albrecht Dürer (Dürer and Strauss, 1977) were both fascinated with the problem of pentagonal tiling and discovered a number of additional shapes which can be combined with the pentagon and decagon to tile the plane.

The idea of tiling polygons derived from the pentagon and decagon formed the basis of a methodology proposed by E.H. Hankin for the construction of Islamic star patterns which he named “polygons in contact” (Hankin, 1925). Building on this, physicists Peter Lu and Paul Steinhardt examined the connection between Islamic patterns and then recently-discovered quasi-periodic crystals which exhibit ordered structures without periodic repetition (Lu and Steinhardt, 2007). Lu and Steinhardt highlight a set of tiles which have come to be known as girih tiles [fig 3]. These can be used in combination to endlessly tile the two-dimensional plane without gaps.

Although there is no definitive extant evidence of a specific methodology as to how these patterns were constructed historically, one of the most important documents available to us in understanding Islamic geometric patterns is the Topkapı Scroll, a 15th century design guide discovered in 1986 and currently housed in the Topkapı Palace Museum, Istanbul. This does not outline specific methods of construction but provides clues which have been analysed and interpreted, most notably by Gülru Necipoğlu (Necipoğlu, 1996).

The dotted red lines marked into the drawing from the Topkapi Scroll [fig 4] indicate a girih tiling which suggests that this approach was known about and used creatively by Islamic designers and craftsmen at least 600 hundred years ago. This set of shapes have internal angles which are multiples of 36º (1/10 of a circle) and can be used to fill the two-dimensional plane in an infinite variety of ways. Inscribing decorative lines into these tiles so that they meet at a consistent angle at the midpoint of the edges, allows for the generation of complex pattern designs [fig 5].
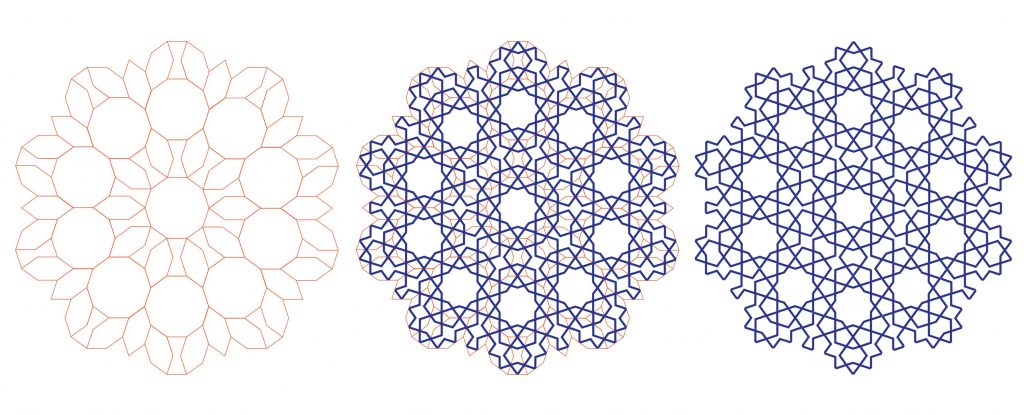
Having studied these references as the basis of a generative system for a family of endlessly variable patterns based on fivefold rotational symmetry, I realized that printmaking would be an ideal method for exploring the possibilities of this modular tiling system. As printmaking is a naturally reflective process which allows for a visual understanding to develop through the act of making it is an ideal vehicle for geometric exploration, a similarly reflective process which allows one to connect directly with, and experience, the visual expression of number in space. Using a laser-cutter I was able to accurately and quickly generate duplicates of all the tiles in a format which lends itself well to relief printing. [fig 6].


From the first print I made in this series [fig 7], I noticed how the visible edges of the girih tiles interrupted the flow of the pattern in the printed image. This reminded me of an exploration of fivefold patterns which I had seen in an appendix in Daud Sutton’s book (Sutton, 2007) focussing on the shapes which make up the patterns. The vocabulary of shapes shown in fig 8 form the basis of another modular approach to generating patterns, one which ignores the invisible underlying girih tiling and focuses on the pattern modules themselves. The vocabulary is simple but the possibilities of the language are complex.

Application of the vocabulary

Having defined this geometric vocabulary of shapes, I began to explore the languages of pattern derived from the interconnected forms. By sticking the individual acrylic tiles to an adhesive backing to generate larger designs I found a solid system for creating relief prints of the designs.
Printing from laser-cut tiles has a further connection to language since the process of composing tiles into designs correlates with the use of letterpress to compose and print sentences from type. The resulting designs also bring to mind the composition of words into poetry or notes into music. The application of colour relates to the use of intonation in spoken language and the timbre of sound, elevating a composition into a more expressive realm. Bringing together the universality of the forms which make up the vocabulary with the potential for creative expression through medium and colour allows the artist to add their own voice to communicate timeless concepts.

In undertaking a hand-drawn compass and straightedge construction the designer strives for perfection but naturally, this is impossible to achieve. Although craftsmanship in the use of digital tools is often overlooked, digital versions of these systematic repeating patterns can result in lifeless renditions as the vibrancy of the human touch can be lost. Moving from the digital back to the analogue by composing and printing the digitally-fabricated tiles by hand re-introduces some inconsistency and vibration to the outcome. In my creative practice, I often oscillate between digital and analogue processes, a smudgy area filled with potential.


A further, closely related vocabulary can be developed by applying different angles to the edges of the tiles [fig 11]. Fig 12 presents the two vocabularies along with four extra shapes which bridge the gap between the two and allow for patterns combining both. With an extended vocabulary of shapes cut as acrylic tiles, I was able to turn to the practical exploration of the rich possibilities of these forms as a visual language through the medium of print.

It is highly possible that craftsmen of the past pieced the elements of this vocabulary together like a puzzle as an alternative method to compass and straightedge construction for pattern discovery, especially when working with pre-cut ceramic tiles. But whereas the compass and straightedge approach encourages the subdivision of the whole starting with a regularly-divided circle, a modular, puzzle-like approach works the other way round, starting with the pieces and assembling the whole. I have found that working from the whole to the many or from the many to the whole results in a different experience and different understanding of the underlying geometry. Relating the modular approach to the more recent technologies of printmaking and digital fabrication has, for me, been a fruitful way of translating theoretical understanding into practical artistic application.
These vocabularies have certain qualities which give them such diverse potential while retaining elegant simplicity. The pentagon and decagon, which form the basis of these vocabularies, are intimately connected with phi, the incommensurable number which defines the familiar proportion known as the Golden Section. An incommensurable, or irrational, number is one which cannot be precisely defined as a decimal number and will resolve to an infinite number of non-repeating decimal places.
The connections between the Golden Section, Fibonacci sequence and natural form have been widely discussed. Their use as a fundamental aspect of composition stretches throughout the history of art and architecture (c.f. Olsen, 2009, Elam, 2001). The Golden Section was described as the Divine Proportion in the book of the same name by Luca Pacioli and Leonardo Da Vinci, perhaps because it governs the structure of many naturally occurring phenomena, from the proportions of the human figure (as described in Da Vinci’s drawing Vitruvian Man) to the movement of planets. Plato considered the Golden Section to be the key to the cosmos and the most important of all mathematical relationships. That this single defining, continuous proportion underpins the fivefold family of patterns gives us an insight into the reason why the resulting vocabularies are so succinct, yet diverse in their application.
As well as providing a simple vocabulary of shapes which can be configured in countless different ways, the inherent golden relationships lead us to self-similar patterns where we can see the same forms appear at different scales within one pattern (as shown in bold red lines in fig 4 and in the design in fig 14). This is an example of meaning powerfully and simply conveyed through the visual medium. The macrocosm is represented in the microcosm, similar to how the spiral of a galaxy is mirrored in the spiral of a snail shell.

A different language developed in a different place
In Morocco, geometric design developed a related but different preoccupation based on fourfold symmetry rather than fivefold. The resulting vocabulary is derived from the eight-pointed star (Castéra, Peuriot and Ploquin, 1999). Mathematically, these forms are based on another incommensurable number, √2. If the side of a square is defined as 1, application of Pythagoras’ theorem tells us that the diagonal is √2. The interaction between 1 and √2 provides the basis for another immensely rich language of forms. The ratio 1:1+√2 is a less well known but equally versatile source of ornamental design known as the Silver Ratio (Weisstein, 2019). It contains similar scaling qualities to the Golden Section but is intimately connected to the square and octagon rather than the pentagon and decagon.
I applied a similar process to this alternate vocabulary, again laser-cutting tiles and relief printing from these to develop an understanding of its inherent qualities.

Schwaller de Lubicz discusses the idea that numbers have qualities as well as the more obvious quantities they represent (Schwaller de Lubicz, 1987). The qualitative difference between eight and ten is apparent in the different visual rhythms that present themselves in these patterns when compared to the fivefold system.
Within the confines of a structured system like language it is possible to express new ideas and through exploration of these geometric vocabularies as a visual language I have discovered a rich source of creative expression.

Conclusion
The interplay of digital and analogue processes in this project creates a dialogue through which unique processes and outcomes arise. Through undertaking this visual research I have found that the analogue and the digital, the traditional and the contemporary, the contemplative and the analytical, are not opposing elements but complementary ones which allow for a full and deep exploration of geometry as a creative language. By engaging in this process and taking these points into consideration I have been able to transform theoretical understanding into practical application.
The beauty of geometry as the foundation of a lexicon of design is its ability to represent the number patterns that govern the structure of the universe. It is through the artistic analysis and application of this geometric lexicon that we come to understand the visual qualities of number in space and their meaning; to express something of the harmonious beauty of nature and to encourage the contemplation of it. The ever-expanding possibilities in methods of application and expression of these forms, both traditional and contemporary, present to the creative artist an inexhaustible resource with which to do this.
References
Bragdon, C. (1915). Projective Ornament. Rochester, NY: The Manas Press, p7.
Burckhardt, T. and Michaud, R. (1976). Art of Islam; Language and Meaning. [London]: World of Islam Festival Publishing Co. Ltd.
Byrne, O. And Oechslin, W. (2010). The first six books of The Elements of Euclid. Köln: Taschen.
Castéra, J., Peuriot, F. and Ploquin, P. (1999). Arabesques. Courbevoie: ACR.
Dürer, A. And Strauss, W. (1977). The Painter’s Manual. New York: Abaris Books.
Elam, K. (2001). Geometry of Design. New York, N.Y.: Princeton Architectural Press.
El-Said, I. and Parman, A. (1976). Geometric concepts in Islamic art. London: World of Islam Festival Trust and Scorpion Pub.
Hankin, E. H. (1925). The Drawing of Geometric Patterns in Saracenic Art. Memoirs of the Archaeological Survey of India, Government of India, Central Publications Branch.
Kepler, J., Aiton, E., Duncan, A. and Field, J. (1997). The Harmony of the World. [Philadelphia, Pa.]: American Philosophical Society.
Lu, P. and Steinhardt, P. (2007). Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture. Science, 315(5815).
Necipoğlu, G. (1996). The Topkapı Scroll – Geometry and Ornament in Islamic Architecture, Santa Monica: Getty Center for the History of Art and the Humanities.
Olsen, S. (2009). The Golden Section. Glastonbury, Somerset: Wooden Books.
Pacioli, L. (2014). de Divina Proportione (on the Divine Proportion): Facsimile (in Black and White) of the Original Version of 1509. Createspace Independent Publishing Platform.
Plato., Lee, H. and Johansen, T. (2008). Timaeus and Critias. London: Penguin.
Schwaller De Lubicz, R. (1987). A Study of Numbers: A Guide to the Constant Creation of the Universe, Rochester, Vt.: Inner Traditions International.
Sutton, D. (2007). Islamic Design. Glastonbury, Somerset: Wooden Books, p54.
Weisstein, E. (2019). Silver Ratio — from Wolfram MathWorld. [online] Mathworld.wolfram.com. Available at: http://mathworld.wolfram.com/SilverRatio.html
Wichmann, B. and Wade, D. (2017). Islamic Design: A Mathematical Approach. Cham: Springer International Publishing.
Copyright for all images and illustrations belongs to the author: © Ameet Hindocha 2019.

